Building Neural Networks in TensorFlow¶
How to use TensorFlow's low-level API to implement a convolutional neural network for machine vision.¶
Google's TensorFlow deep-learning API is a powerful tool that lets us take full advantage of the parallel processing capabilities offered by Graphical Processing Units (GPUs). With TensorFlow, we can train our neural networks faster, with greater control over our data processing pipeline.
This tutorial introduces TensorFlow through its low-level API. While it's possible to jump straight to higher-level APIs like Keras which use TensorFlow as a backend, working first with the lower-level API gives us a better idea of what's going on under the hood, which is useful for debugging and customization later on.
To demonstrate the use of TensorFlow, we'll implement a convolutional neural network (CNN) that allows a computer to recognize handwritten digits. CNNs are a popular and powerful approach to many image-based classification tasks.
Dataset:¶
We will be using the well-known MNIST dataset found here. The training set consists of handwritten digits from 250 different people: 50% were high school students and 50% were employees from the census bureau.
GPU Specifications:¶
The GPU used in this demonstration is the NVIDIA GeForce GTX 1060:
- 1280 cores @ 1544 MHz base
- 6GB GDDR5 memory @ 8008 MHz, 192-bit bus
The manufacturer was MSI. Seen in my computing rig below:

Import Python Libraries:¶
import os
import struct # methods for unpacking binary data
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from PIL import Image # python image manipulation library
# set Jupyter Notebook options
%matplotlib inline
1. Importing the Image Dataset¶
The MNIST image set is provided as binary data. We'll define a function below for unpacking it.
The 60,000 training images and labels are contained in the files train-images.idx3-ubyte and train-labels.idx1-ubyte respectively.
The 10,000 test images and labels are found in t10k-images.idx3-ubyte and t10k-labels.idx1-ubyte.
# define a function for unpacking the datasets
def load_mnist(path, dataset_type='train'):
labels_path = os.path.join(
path, '%s-labels.idx1-ubyte' % dataset_type)
with open(labels_path, 'rb') as lbpath:
magic, n = struct.unpack('>II', lbpath.read(8))
# note: '>II' defines the byte sequence for unpacking
labels = np.fromfile(lbpath, dtype=np.uint8)
# note: reads data into a numpy array
images_path = os.path.join(
path, '%s-images.idx3-ubyte' % dataset_type)
with open(images_path, 'rb') as imgpath:
magic, num, rows, cols = \
struct.unpack('>IIII', imgpath.read(16))
# note: 'magic' gives the file protocol
images = np.fromfile(
imgpath, dtype=np.uint8).reshape(len(labels), 784)
return images, labels
Next we specify the filepath, load the dataset, and print the dataset shapes to verify.
mnist_path = './data/mnist/'
X_train, y_train = load_mnist(mnist_path, dataset_type='train')
X_test, y_test = load_mnist(mnist_path, dataset_type='t10k')
print('Training Set --> Rows: %d, Columns: %d' % \
(X_train.shape[0], X_train.shape[1]))
print('Test Set --> Rows: %d, Columns: %d' % \
(X_test.shape[0], X_test.shape[1]))
2. Data Visualization¶
Let's print several instances of each digit to see some of the differences in writing style.
# create a subplot array, with each column a different digit,
# and each row a different instance
fig, ax = plt.subplots(nrows=5, ncols=10,
sharex=True, sharey=True,
figsize=(14, 8))
ax = ax.flatten()
for i in range(5):
for j in range(10):
# reshape into original 28x28 pixel grid
img = X_train[y_train == j][i].reshape(28, 28)
ax[10*i + j].imshow(img, cmap='Greys',
interpolation='nearest')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.show()
Some of the digits in our dataset are challenging to categorize even for a human. For example, in the set of 5's displayed below, the first and seventh images could easily be mistaken as a 3.
fix, ax = plt.subplots(nrows=1, ncols=10,
sharex=True, sharey=True,
figsize=(14, 8))
ax = ax.flatten()
for i in range(10):
img = X_train[y_train == 5][i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.show()
Introducing CNNs:
Convolutional Neural Networks (CNNs) employ feature heirarchy: the early layers at the input extract low-level features (e.g. edges, corners), while the later layers combine these to form higher-level features (e.g. shapes, objects). A typical CNN consists of convolutional (conv) layers, subsampling through pooling layers, and one or more fully-connected layers (e.g. a multilayer perceptron) at the end. Both the convolutional and fully-connected layers have weight parameters and biases that are 'learned' as we train our CNN.
An excellent introductory video explaining the basics of CNNs can be found at this link. Roughly speaking, we can think of the convolution operations as sliding a 'filter' across the layer input. These filters specialize in detecting different features. Some might produce a large output value when they slide over corners; others might produce a large output when they slide over edges of a specific orientation, etc. Usually each convolution layer has several output channels, each of which come to specialize in detecting different low-level features.
The CNN architecture we will use is illustrated in the diagram below and is relative simply. For a primer on more advanced CNN architectures including many important recent developments, I recommend reading the papers mentioned here.
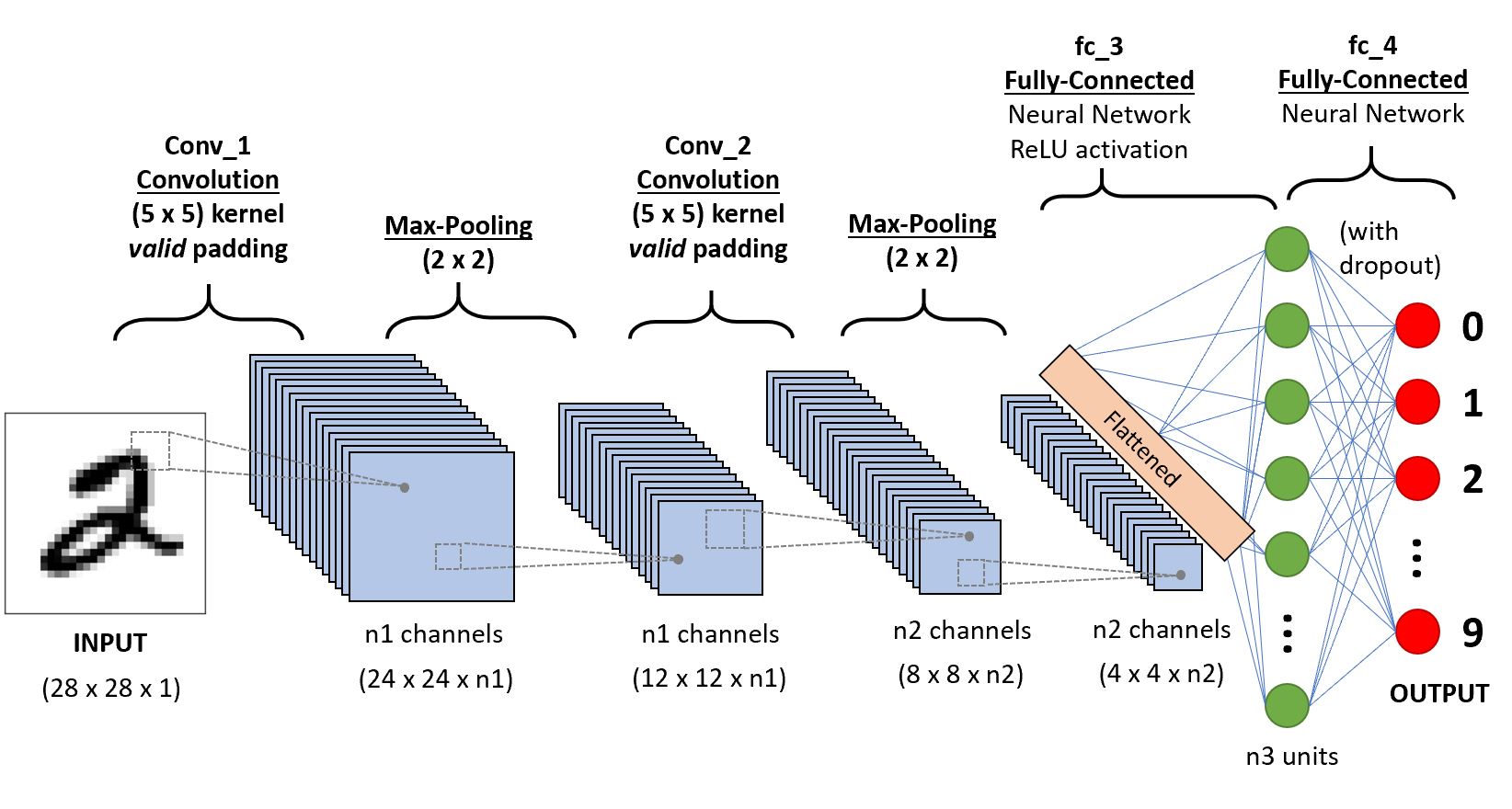
Our simple CNN will consist of two convolutional layers (using 5x5-pixel kernels and "valid"-type padding where we drop the perimeter pixels) each followed by max-pooling layers having 2x2 downsampling. Next we'll flatten the output channels into vectors and feed these to a fully connected layer (fc_3) having a Rectified Linear Unit (ReLU) activation function, followed by a second fully-connected layer (fc_4) to whose output we'll apply the softmax function to determine the most probable class label (i.e. which digit between 0 and 9). Between layers fc_3 and fc_4, we'll apply a popular regularization technique called 'dropout' to help prevent overfitting. A fraction of our hidden units (optimally 50%) will be randomly dropped with each training iteration, which forces our network to learn more general and robust patterns from the training data.
Our CNN has several hyperparameters, including:
- learning rate
- convolutional kernel size and padding type
- max-pooling strides
- number of output channels after each conv layer
- number of units in the fc_3 layer
Some of these we'll hard-code, others we'll set as variables. Note that the dropout rate is also technically a hyperparameter, but in this case it's already understood to be optimal at 50%.
Batch Generator:
Let's first define a helper function that splits our total training set into mini-batches that we train our CNN on sequentially. There are two main reasons for doing this:
The use of mini-batches injects some noise into our gradient-based updates to model parameters (e.g. the weights between nodes in our network), helping us escape local minima and thereby optimize to a better-performing model.
GPUs generally have less available RAM than CPUs, which can be a problem for large datasets.
# define a function for iterating through mini-batches of the data
def batch_generator(X, y, batch_size=100,
shuffle=False, random_seed=None):
ind = np.arange(y.shape[0]) # create indices
if shuffle: # shuffles sample order in output batch
rng = np.random.RandomState(random_seed) # random num gen
rng.shuffle(ind) # use random nums to shuffle indices
X = X[ind]
y = y[ind]
for i in range (0, X.shape[0], batch_size):
yield (X[i:i+batch_size, :], y[i:i+batch_size])
Implementing the CNN in Low-Level TensorFlow:
TensorFlow provides an interface between easy-to-use Python and the more tempermental and tricky C++ that is used to communicate with the GPU.
We'll define our CNN as a class, using TensorFlow's low-level API. The core idea is that we first define a computational graph that gets compiled and run during a TensorFlow session. This graph consists of all tensors, variables, layers, and arithmetic involved in our model definition. To feed data into our network, we must pre-define data placeholders, which we feed with dictionaries containing our data during training. Prior to running any calculations, all variables in our computational graph must first be initialized.
The following commented code walks you through the process of building a model object using TensorFlow, including methods for saving and loading the model parameters.
class DigitCNN(object):
def __init__(self, batchsize=100,
epochs=10, learning_rate=1e-4,
conv_1_output_channels=32,
conv_2_output_channels = 64,
dropout=0.5, fc_3_output_units=1024,
shuffle=True, random_seed=None):
np.random.seed(random_seed)
# seeds np for reproducability
# between identical training instances
self.batchsize = batchsize
# how many training samples we feed to
# our GPU at a time
self.epochs = epochs
# number of training epochs
self.learning_rate = learning_rate
# scales the weight updates
self.conv_1_output_channels = conv_1_output_channels
# num output channels from Conv_1 layer
self.conv_2_output_channels = conv_2_output_channels
# num output channels from Conv_2 layer
self.fc_3_output_units = fc_3_output_units
# num output units from Fully-Connected layer 3
self.dropout = dropout
# dropout probability for neurons in our FC layers
self.shuffle = shuffle
# if True, shuffles the training samples between epochs
self.history = pd.DataFrame(
columns=['Epoch','Loss','Accuracy'])
# for tracking performance
# TensorFlow needs to construct the computational graph
# before we begin feeding it data:
self.g = tf.Graph()
with self.g.as_default():
# set TensorFlow's random seed to match that of numpy
tf.set_random_seed(random_seed)
# construct the graph for our CNN
self.build()
# initialize the values of any variables
# we have explicitly defined in our graph
self.init_op = tf.global_variables_initializer()
# TensorFlow's saver; will be used to
# save the CNN variables after training
self.saver = tf.train.Saver()
# create a TensorFlow session using
# our computational graph
self.sess = tf.Session(graph=self.g)
# *** defines the computational graph built for our CNN ***
def build(self):
# define placeholders for X (images) and y (labels),
# which we will feed data into later
tf_x = tf.placeholder(
dtype=tf.float32,
shape=[None, 28*28],
name='tf_x')
tf_y = tf.placeholder(
dtype=tf.int32,
shape=[None],
name='tf_y')
# since we feed X in as batches, we must
# reshape it into a Rank 4 tensor,
# tensor dimensions: [batchsize, width, height, 1]
# notes:
#- the last digit specifies the number of
# channels (3 for RGB, 1 for greyscale)
# - 28x28 comes from the number of pixels
# - specifying -1 for a dimension tells TF
# to compute it based on existing constraints
tf_x_image = tf.reshape(
tf_x,
shape=[-1, 28, 28, 1],
name='input_x_2dimages')
# one-hot encoding assigns labels 0-9
# their own basis vectors, e.g. [1, 0, 0 ...]
tf_y_onehot = tf.one_hot(
indices=tf_y,
depth=10,
dtype=tf.float32,
name='input_y_onehot')
# ** We begin building up our convolutional neural network **
# first layer: Conv_1 (convolutional)
print('\nBuilding Conv_1 Layer:')
h1 = self.conv_layer(
tf_x_image, name='conv_1',
kernel_size=(5, 5),
padding='VALID',
n_output_channels=self.conv_1_output_channels)
# MaxPooling of Conv_1
h1_pool = tf.nn.max_pool(
h1,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='SAME')
# second layer: Conv_2 (convolutional)
print('\nBuilding Conv_2 Layer:')
h2 = self.conv_layer(
h1_pool, name='conv_2',
kernel_size=(5, 5),
padding='VALID',
n_output_channels=self.conv_2_output_channels)
# MaxPooling of Conv_2
h2_pool = tf.nn.max_pool(
h2,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='SAME')
# third layer: fc_3 (fully-connected)
print('\nBuilding fc_3 layer:')
h3 = self.fc_layer(
h2_pool, name='fc_3',
n_output_units=self.fc_3_output_units,
activation_fn=tf.nn.relu)
# note: relu = rectified linear unit
# neuron dropout for fc_3
# (we will feed this a value)
keep_prob = tf.placeholder(
tf.float32,
name='fc_keep_prob')
h3_drop = tf.nn.dropout(
h3, keep_prob=keep_prob,
name='dropout_layer')
# fourth layer: fc_4 (fully-connected)
print('\nBuilding 4th layer:')
h4 = self.fc_layer(
h3_drop, name='fc_4',
n_output_units=10, # matches num. unique labels
activation_fn=None) # we use linear activation here
# ** now we add to our computational graph
# all the other functions needed to perform
# training, predictions, and validation **
# generate probabilities with softmax,
# and take the logit with largest activation
# as the class
predictions = {
'probabilities': tf.nn.softmax(h4,
name='probabilities'),
'labels': tf.cast(tf.argmax(h4, axis=1),
tf.int32, name='labels')}
# we will use softmax cross entropy
# as our loss function (to be minimized)
cross_entropy_loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits_v2(
logits=h4, labels=tf_y_onehot),
name='cross_entropy_loss')
# we'll perform optimization using the
# AdamOptimizer, a robust and popular
# gradient-based method
optimizer = tf.train.AdamOptimizer(self.learning_rate)
optimizer = optimizer.minimize(
cross_entropy_loss,
name='train_op')
# getting the number of correct
# predictions and corresponding accuracy
correct_predictions = tf.equal(
predictions['labels'],
tf_y, name='correct_preds')
accuracy = tf.reduce_mean(
tf.cast(correct_predictions, tf.float32),
name='accuracy')
# *** create Wrapper for convolution layers ***
def conv_layer(self, input_tensor, name,
kernel_size, n_output_channels,
padding='SAME', strides=(1, 1, 1, 1)):
with tf.variable_scope(name):
# note: input tensor shape is [batchsize,
# width, height, input_channels]
input_shape = input_tensor.get_shape().as_list()
n_input_channels = input_shape[-1]
weights_shape = list(kernel_size) \
+ [n_input_channels, n_output_channels]
weights = tf.get_variable(
name='_weights',
shape=weights_shape)
print(weights)
biases = tf.get_variable(
name='_biases',
initializer=tf.zeros(shape=[n_output_channels]))
print(biases)
conv = tf.nn.conv2d(
input=input_tensor,
filter=weights,
strides=strides,
padding=padding)
print(conv)
conv = tf.nn.bias_add(
conv,
biases,
name='net_pre-activation')
print(conv)
conv = tf.nn.relu(conv, name='activation')
print(conv)
return conv
# *** create wrapper for fully-connected layers ***
def fc_layer(self, input_tensor, name,
n_output_units, activation_fn=None):
with tf.variable_scope(name):
input_shape = input_tensor.get_shape().as_list()[1:]
# everything but batch size
n_input_units = np.prod(input_shape)
if len(input_shape) > 1:
input_tensor = tf.reshape(
input_tensor,
shape=(-1, n_input_units))
weights_shape = [n_input_units, n_output_units]
weights = tf.get_variable(
name='_weights',
shape=weights_shape)
print(weights)
biases = tf.get_variable(
name='_biases',
initializer=tf.zeros(shape=[n_output_units]))
print(biases)
layer = tf.matmul(input_tensor, weights)
print(layer)
layer = tf.nn.bias_add(
layer,
biases,
name='net_pre-activation')
print(layer)
if activation_fn is None:
return layer
layer = activation_fn(layer, name='activation')
print(layer)
return layer
# *** saving the model ***
def save(self, epoch, path='./digitCNN-model/'):
if not os.path.isdir(path):
os.makedirs(path)
print('Saving model in %s' % path)
self.saver.save(
self.sess,
os.path.join(path, 'model.ckpt'),
global_step=epoch)
# *** loading the model from saved data ***
def load(self, epoch, path):
print('Loading model from %s' % path)
self.saver.restore(
self.sess,
os.path.join(path, 'model.ckpt-%d' % epoch))
# *** training the CNN ***
def train(self, training_set,
validation_set=None, initialize=True):
# initialize variables
if initialize:
self.sess.run(self.init_op)
X_data = np.array(training_set[0])
y_data = np.array(training_set[1])
epoch0 = self.history['Epoch'].shape[0]
# how many epochs have already been trained
for epoch in range(1, self.epochs + 1):
batch_gen = batch_generator(X_data,
y_data,
shuffle=self.shuffle)
avg_loss = 0.0
for i, (batch_x,batch_y) in enumerate(batch_gen):
feed = {'tf_x:0': batch_x,
'tf_y:0': batch_y,
'fc_keep_prob:0': self.dropout} # for dropout
loss, _ = self.sess.run(
['cross_entropy_loss:0', 'train_op'],
feed_dict=feed)
avg_loss += loss
print('Epoch %02d: Training Avg. Loss: %7.3f' \
% (epoch, avg_loss), end=' ')
# check accuracy on validation set if supplied
if validation_set is not None:
feed = {'tf_x:0': validation_set[0],
'tf_y:0': validation_set[1],
'fc_keep_prob:0': 1.0}
# we DON'T want neuron dropout when making predictions
valid_acc = self.sess.run('accuracy:0', feed_dict=feed)
print(', Validation Acc: %7.3f' % valid_acc)
# update our CNN's performance history
self.update_history((epoch0 + epoch,
avg_loss,
valid_acc))
else:
self.update_history((epoch0 + epoch, avg_loss))
print()
# *** making predictions with our trained CNN ***
def predict(self, X_test, return_proba=False):
feed = {'tf_x:0' : X_test,
'fc_keep_prob:0': 1.0}
# we DON'T want neuron dropout when making predictions
if return_proba:
return self.sess.run('probabilities:0',
feed_dict=feed)
else:
return self.sess.run('labels:0',
feed_dict=feed)
# *** exporting log files that allow us to
# visualize our graph using TensorBoard ***
def export_logs(self):
self.sess.run(self.init_op)
file_writer = tf.summary.FileWriter(
logdir='./logs/',
graph=self.g)
# *** updating our CNN's performance history ****
def update_history(self, entry):
# note: entry is a typle of form
# (epoch_number, avg_loss, valid_acc)
if len(entry) is 3:
# case where we provided a
# validation set to compute accuracy
new_entry = pd.DataFrame(
columns=['Epoch', 'Loss', 'Accuracy'])
new_entry.loc[0] = [entry[0], entry[1], entry[2]]
else:
new_entry = pd.DataFrame(columns=['Epoch', 'Loss'])
new_entry.loc[0] = [entry[0], entry[1]]
# refresh the dataframe row indexing
self.history = self.history.append(new_entry)
self.history = self.history.reset_index(drop=True)
Note that I have chosen to stick with TensorFlow's low-level API. Some of the above steps can be simplified by making use of its higher-level Layers API.
Let's now initialize an instance of our newly-defined CNN class. We'll set its training to 30 epochs. Creating our CNN object and building the computational graph:
cnn = DigitCNN(epochs=30, random_seed=27)
TensorFlow has a handy tool called TensorBoard which can be used to visualize computational graphs. First we must export the graphs as follows:
# create graph log to visualize with TensorBoard
cnn.export_logs()
Instructions on how to use TensorBoard can be found here. Below we view the computational nodes connected to each of our layers:
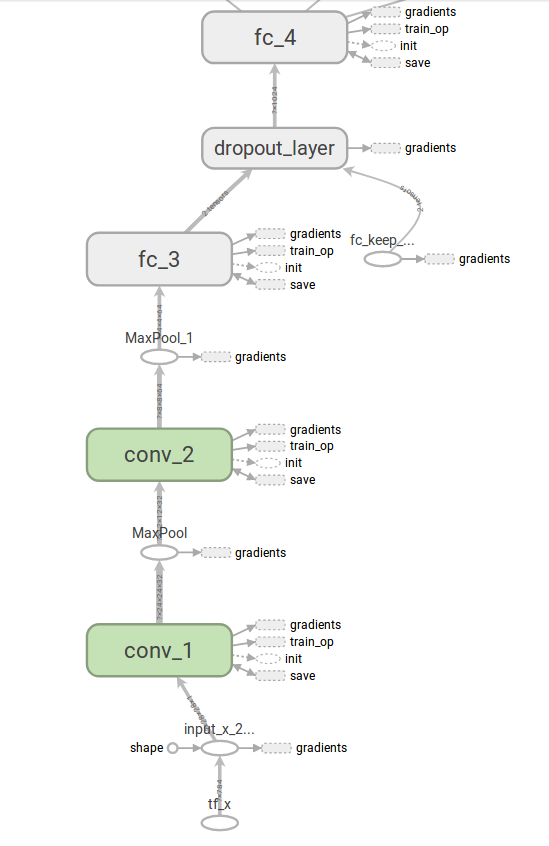
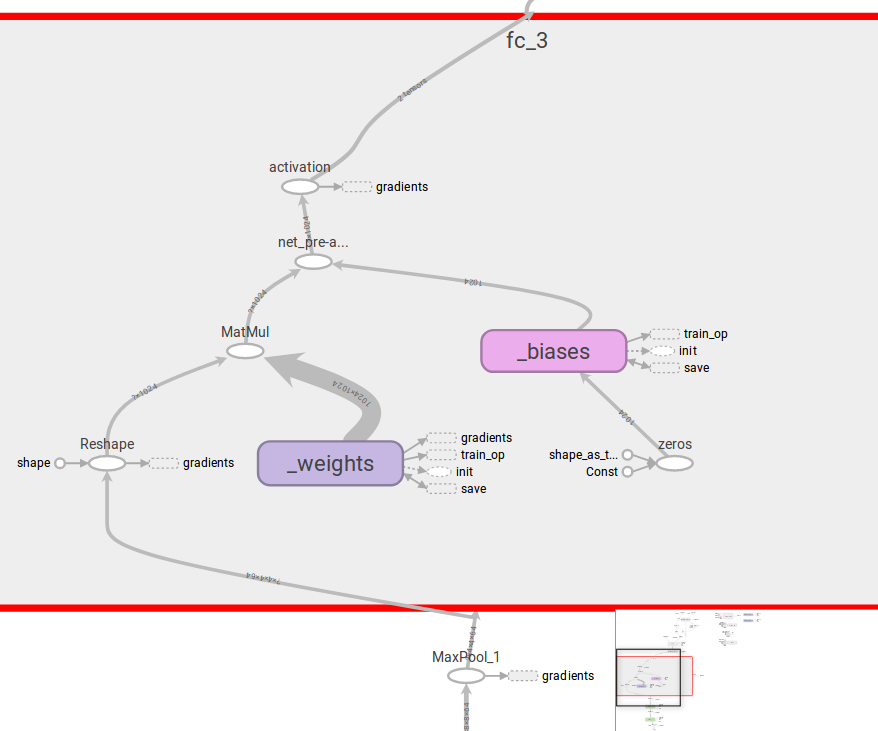
We can also expand each layer (in this case fc_3) to see a more detailed breakdown of the computational nodes within:
Before training our CNN, we must standardize our data. We'll also create a validation set using the last 10000 samples of our 60000-sample training set. (Note that we would typically use k-fold cross validation.)
# we then need to normalize the data (mean centering
# and division by the standard deviation) for better
# training performance and convergence
mean_vals = np.mean(X_train, axis=0)
std_val = np.std(X_train)
# obtain the standardized version of our data:
X_train_standardized = (X_train - mean_vals)/std_val
X_test_standardized = (X_test - mean_vals)/std_val
# instead of k-fold cross-validation, we'll just
# use the last 10000 training entries
X_train_standardized_subset, y_train_subset = \
X_train_standardized[:50000,:], y_train[:50000]
X_valid_standardized, y_valid = \
X_train_standardized[50000:,:], y_train[50000:]
Next we train our CNN and save the fitted model.
# train our neural network
cnn.train(training_set=(X_train_standardized_subset,
y_train_subset),
validation_set=(X_valid_standardized,
y_valid),
initialize=True)
# save the model after training
cnn.save(epoch=30)
Now let's print the loss function (cross-entropy) and training accuracy, as a function of the number of training epochs:
plt.rcParams.update({'font.size': 16})
fig, ax1 = plt.subplots(figsize=(12, 6))
ax1.plot(cnn.history['Epoch'].values,
cnn.history['Loss'].values, 'r-')
ax1.set_xlabel('Training Epochs')
ax1.set_ylabel('Loss Function', color='r')
ax1.tick_params('y', colors='r')
ax2 = ax1.twinx()
ax2.plot(cnn.history['Epoch'].values,
cnn.history['Accuracy'].values, 'b-')
ax2.set_ylabel('Validation Accuracy',
color='b', labelpad=20)
ax2.tick_params('y', colors='b')
fig.tight_layout()
plt.show()
After 30 training epochs the model is at or near convergence for this set of hyperparameters. At this point we could choose to tune our model hyperparameters to see if the model performance can be further improved. This could be done, for example, by performing a grid search while using k-fold cross-validation.
For now, let's continue with the present hyperparameter set and retrain our CNN using the full training set (including the samples we used for obtaining validation accuracy), in preparation for determining the test set accuracy.
cnn.train(training_set=(X_train_standardized, y_train),
initialize=True)
# obtain predictions for test set
y_test_preds = cnn.predict(X_test_standardized)
# print model's accuracy
print('Test Accuracy: %.2f%%' % \
(100*np.sum(y_test == y_test_preds)/len(y_test)))
# let's look at some examples
print('\nClassification Examples: (predicted class is shown below image)')
fix, ax = plt.subplots(nrows=1, ncols=10,
sharex=True, sharey=True,
figsize=(14, 8))
ax = ax.flatten()
for i in range(10):
img = X_test_standardized[:10][i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_xlabel(y_test_preds[:10][i])
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()
# print(cnn.predict(X_test_standardized[:10, :]))
Let's examine some of the cases where our model classified the data incorrectly:
print('Misclassified Digits:')
fig, ax = plt.subplots(nrows=1, ncols=10,
sharex=True, sharey=True,
figsize=(14, 8))
ax = ax.flatten()
mscls = [y_test_preds != y_test] # indices of misclassified digits
for i in range(10):
img = X_test_standardized[mscls][i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_xlabel('%s (was %s)' % \
(y_test_preds[mscls][i], y_test[mscls][i]))
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()
It's easy to see how even a human might have difficulty identifying some of these examples, hence it's not surprising they were misclassified.
Next I photographed my own handwriting to see how well our CNN's performance generalizes to an unseen writing style. The digit images were manually rescaled, centered, and cropped prior to being loaded below:
# specify the path of our custom digits
imagepath = './myDigits_v2/'
# we need to invert the pixels to harmonize
# format with our training data
def invert_png(pixel):
return np.absolute(pixel - 65535)
invert_png = np.vectorize(invert_png)
# load the image files and assign class labels
my_digits_X = []
my_digits_y = []
for file in os.listdir(imagepath):
img = Image.open(os.path.join(imagepath, file))
pix = np.array(img)
pix_inv = invert_png(pix)
my_digits_X.append(pix_inv.reshape(784))
my_digits_y.append(int(file[0]))
# note: first character in filename identifies class
my_digits_X = np.array(my_digits_X)
my_digits_y = np.array(my_digits_y)
# sort the images in ascending order
sorted_ind = np.argsort(my_digits_y)
my_digits_X = my_digits_X[sorted_ind]
my_digits_y = my_digits_y[sorted_ind]
# display the imported digits
fig, ax = plt.subplots(nrows=1, ncols=10,
sharex=True, sharey=True,
figsize=(14, 8))
ax = ax.flatten()
for i in range(10):
img = my_digits_X[i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_xlabel('%s' % my_digits_y[i])
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()
Next I standardize these digits, obtain digit predictions from our CNN, and display the classification results:
# standardize the data
mean_vals = np.mean(my_digits_X, axis=0)
std_val = np.std(my_digits_X)
my_digits_X_standardized = (my_digits_X - mean_vals)/std_val
# obtain predictions for test set
my_digits_y_preds = cnn.predict(my_digits_X_standardized)
# print model's accuracy on the input data
print('Test Accuracy: %.2f%%' % \
(100*np.sum(my_digits_y == my_digits_y_preds)/len(my_digits_y)))
# plot the results
print('\nClassification Results: (predicted class is shown below image)')
fix, ax = plt.subplots(nrows=1, ncols=10,
sharex=True, sharey=True,
figsize=(14, 8))
ax = ax.flatten()
for i in range(10):
img = my_digits_X_standardized[:10][i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_xlabel(my_digits_y_preds[:10][i])
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()
In this case our CNN yielded 100% accuracy!
In general there several techniques for assessing how well a model generalizes to unseen data, such as through learning curves.
Closing Remarks¶
In this tutorial, we saw how to use TensorFlow's low-level API to define a convolutional neural network for handwritten digit recognition. By now you should have a basic understanding of how TensorFlow works and how to use it for training your own models.
More recently, the use of placeholders and feed dictionaries has been superceded by the newer Dataset API, which allows us to utilize the same input pipeline across all of our models. Complementary to this are the introduction of new methods for defining feature columns and custom networks (estimators). You can read more about these new paradigms in the following blog posts by the Google team:
- https://developers.googleblog.com/2017/09/introducing-tensorflow-datasets.html
- https://developers.googleblog.com/2017/11/introducing-tensorflow-feature-columns.html
- https://developers.googleblog.com/2017/12/creating-custom-estimators-in-tensorflow.html
Personally, I've found it faster to use Keras for building my models. This cuts down on a lot of cumbersome "boilerplate" code and makes easier to quickly go from idea to experiment. Knowing the lower-level TensorFlow API is nonetheless useful for debugging and can be used to implement more advanced or customized features that exist in TensorFlow but are not part of the Keras frontend.
For a primer on how to use Keras for rapidly prototyping more complex networks, see my tutorial here.